Transcurvatura

La scoperta di Zefram Cochrane della propulsione a curvatura ha cambiato il volto dell'esplorazione spaziale nel XXI secolo. Da allora, la Federazione ha tentato invato di trovare nuovi mezzi per viaggiare a velocità superiori

La fondazione della Federazione Unita dei Pianeti è stata resa possibile dall'invenzione dei motori a curvatura. Grazie a questo dispositivo, le navi stellari possono raggiungere velocità superiori a quella della luce. Con i successivi sviluppi sono state aperte rotte di comunicazione e di rifornimento tra sistemi stellari molto distanti. Ma con la propulsione a curvatura convenzionale la velocità di una nave stellare ha un limite, generalmente fissato a curvatura 9.6. La transcurvatura in teoria permetterebbe di viaggiare a velocità ben superiori. Le leggi della fisica hanno sempre suggerito che sono possibili 'scorciatoie' più dirette, e nel 2369 la Federazione viene a conoscenza di una tecnologia alternativa che viene ribattezzata condotto di transcurvatura.

La fisica della velocità

Il raggiungimento della velocità di curvatura è reso possibile dal meccanismo inventato da Zefrarn Cochrane della propulsione a distorsione del continuum (CDP), che venne soprannominata propulsione a 'curvatura' a causa del modo in cui il campo energetico generato dai motori distorce il continuum spazio-temporale. La distorsione consente alla nave stellare di spostarsi nel subspazio, riducendone la massa e rendendo possibili i viaggi a grandi velocità. La massima velocità di curvatura nel subspazio si avvicina a 2'000 volte quella della luce. In teoria, comunque, sono possibili anche velocità più elevate attraverso la distorsione del subspazio. Questa ipotesi costituisce la base della teoria della transcurvatura. Il grande interesse suscitato da questa teoria è determinato dalla prospettiva delle potenziali, rivoluzionarie applicazioni pratiche che consentirebbero di superare definitivamente le limitazioni imposte dalle tecnologie in uso che, a causa di richieste energetiche eccessive, impediscono ai vascelli stellari di avvicinarsi al limite di Eugene di curvatura 10.
Per comprendere la relazione tra viaggi subluce, a curvatura e a transcurvatura occorre considerare il passaggio di una nave stellare attraverso l'universo. La traiettoria di un oggetto può essere posta su un diagramma spazio-temporale. In questi grafici, su un asse viene indicato il termpo e sull'altro le distanze tra gli oggetti. Le traiettorie appaiono come linee serpeggianti diagonali chiamate geodetiche. Le velocità subluce formano geodetiche 'time-like' sempre inclinate a meno di 45 gradi rispetto alla verticale. I raggi di luce (e le navi stellari che viaggiano a curvatura 1) seguono linee conosciute come geodetiche di lunghezza nulla, che sono precisamente a 45 gradi rispetto alla verticale. Infine, le velocità superiori a quella della luce seguono geodetiche 'space-like' che sono sempre inclinate a più di 45 gradi rispetto alla verticale. Le geo- detiche 'space-like' possono essere ulteriormente suddivise in geodetíche di curvatura e geodetiche di transcurvatura.

Similitudini con i tunnel spaziali

La lunghezza di una geodetica tra due punti della Galassia (per esempio due sistemi stellari) indica quanto spazio-tempo bisogna percorrere per muoversi da un punto all'altro. Su un diagramma spazio-temporale, l'intervallo orizzontale tra i punti è la loro distanza, mentre l'intervallo verticale indica il tempo impiegato per viaggiare.

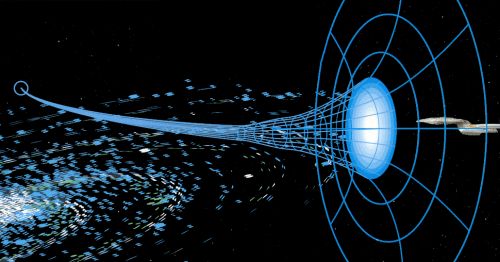I condotti di transcurvatura piegano il tempo e lo spazio, creando un ponte tra sezioni distanti della Galassia e riducendo il tempo necessario per viaggiare fra esse.

Confrontando le geodetiche per andare da un sistema stellare A a uno B, si può vedere il viaggio a transcurvatura come un taglio netto laterale attraverso l'universo in alternativa al percorso completo.
Un altro modo per immaginare un condotto di transcurvatura è quello di pensarlo simile a un tunnel spaziale. Un tunnel spaziale è una distorsione nel continuum spazio-temporale attraverso una dimensione più alta in modo che due regioni distanti dello spazio risultino più vicine. Un condotto di transcurvatura è esattamente lo stesso con la differenza che non viene distorto il continuum spazio-temporale, ma viene piegato su se stesso il subspazio.
Per penetrare nel subspazio e aprire un condotto dallo spazio normale, occorre produrre alcune particelle speciali chiamate tachioni. Queste particelle subatomiche non possono viaggiare a velocità inferiori a quella della luce, perciò seguono geodetiche space-like, rendendo possibili le comunicazioni con altre dimensioni dell'universo quali il sub-spazio. Una volta trovata la corretta frequenza dei tachioni, la foro emissione provoca un'oscillazione in risonanza nel subspazio, che può essere rilevata come una distorsione subspaziale. Questo apre un varco dallo spazio normale attraverso il subspazio, rendendo possibile l'accesso al condotto di transcurvatura. Il flusso di energia subspaziale nel varco è così intenso che ogni cosa nelle vicinanze viene trascinata all'interno e immediatamente accelerata a velocità estreme, come un ramoscello caduto in un fiume viene trascinato via dalla corrente. Dopo una breve corsa movimentata attraverso il condotto, la nave stellare torna nello spazio normale, a molti anni luce dal punto di origine.

Esperimenti con la transcurvatura

Gli scienziati e gli ingegneri della Flotta Stellare, dopo un intenso periodo di lavoro finalizzato allo sviluppo dei principi teorici, ritengono che le loro ipotesi sulla transcurvatura debbano essere finalmente messe alla prova. A questo scopo, nel 2285 viene costruita una nave stellare sperimentale, la U.S.S. Excelsior. Sfortunatamente, però, i test non vanno a buon fine; la Flotta Stellare non riesce a infrangere la barriera della transcurvatura, e il progetto viene abbandonato Nel 2369, comunque, la U.S.S. Enterprise assiste alla creazione di un condotto di transcurvatura durante l'inseguirnento di un vascello borg e lo utilizza, dimostrando così che la teoria può anche essere messa in pratica.